SimpleBlog
Index of all articlesPatterns, what is it what I am looking for?



 ...
... 
As always, I have to warn you, that what follows are the thoughts of a naive mathematican. A serious mathematican will probably say: Hey boy, do real math, every thing you think about, is already described in a consensual and clear form! But for me it’s realy fun to bootstrap my own view of the world out of my hummingbird mind. And sometimes there is this aha feeling!
So, I am a pattern searcher and the math universe is so big (indeed the bigest), that I gave up to undertsand it realy (but still hoping that it makes klick, without any hope that I can ever transform any not trivial equation without a mistake ;-)))
While thinking about a permutation game, I implemented and quadratic spirals, which a long time fascinated me and still do, I got deeper into the concept of permutations (the possible quadratic spirals are 8 specific permutations based on the size of the quadratic matrix and permutation game stands for it self). So I found some texts about group theory and symmetrie and got a naive notion of these concepts.
The spirals brought me to the very naive notion of spiral symmetrie, i.e. binary patterns that map to themself when they are spiralized. I was fascinated about the strange patterns and numbers I found, but as always, if you do no real math, you can only scrap the surface. (By the way: as real mathematican you have the same problem, but your surface is much bigger ;-) After a while I recogniced, that the 8 spiral permutations are only a very small cut-out of possible symmetrie operations.
I think every permutation of n elements founds a symmetrie group over a n-sized pattern.
But, what is a meaningful pattern?
1. Patterns are ordered.
2. It is essential, that the elements of patterns are identifyable and distinguishable if different elements are involved.
3. It is also essential, that individual elements can appear more then one time.
4. There is a hierachy of recursive patterns. But there are atoms, something like patternpatterns. And so:
5. There are sets of abstract atomic patterns, that are n-sized and built from at most n distinguishable elements.
And here they are:
The set of abstract atomic patterns over 1 individual element
 A world with one individual can only form one pattern! I took the colour white for the first individual. Let’s call white 1.
A world with one individual can only form one pattern! I took the colour white for the first individual. Let’s call white 1.
Setsize: 1
The set of abstract atomic patterns over 2 individual elements
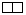
 A world with two individuals can only form 3 patterns! I took the colour black for the second individual. Let’s call black 0.
A world with two individuals can only form 3 patterns! I took the colour black for the second individual. Let’s call black 0.
Setsize: 3
The set of abstract atomic patterns over 3 individual elements
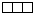

 A world with 3 individuals can only form 10 patterns! I took the colour red for the 3. individual. Let’s call red 2 (this I have to rethink, but if you want countable numbers this makes sense. May be it works with white=0 and black=1 also.)
A world with 3 individuals can only form 10 patterns! I took the colour red for the 3. individual. Let’s call red 2 (this I have to rethink, but if you want countable numbers this makes sense. May be it works with white=0 and black=1 also.)
Setsize: 10
The set of abstract atomic patterns over 4 individual elements
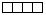


 A world with 4 individuals can only form 47 patterns! New colour green.
A world with 4 individuals can only form 47 patterns! New colour green.
Setsize: 47
The set of abstract atomic patterns over 5 individual elements
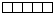





 A world with 5 individuals can only form 246 patterns! New colour blue.
A world with 5 individuals can only form 246 patterns! New colour blue.
Setsize: 246
and so on …
So what’s remarkable?
1. The last subset represents the permutations over n elemnets. So you can use this patterns to check the symmetries over the other subsets.
2. The subsets are based on the partitions of n. So for example: 3 = 3, 2+1, 1+1+1 


3. And so the setsize follows for example 3, with c(x,y) = number of ordered x-sized combinations out of y elements: c(3,3)+ c(2,3) x c(1,1) + c(1,3) x c(1,2) x c(1,1) = Setsize(3) = 10 and for all n: 1, 3, 10, 47, 246, 1602, 11481, 95503, 871030, 8879558 … which is A005651: Sum of multinomial coefficients
4. Symmerties: A lot of work, but for example subset one has always the last sets size symmetries. (but this is trivial)
 muzuu.org ist im Besitz von Kizuu, welche ein Produkt von Zuufuzu ist. Kontakt:
muzuu.org ist im Besitz von Kizuu, welche ein Produkt von Zuufuzu ist. Kontakt: