SimpleBlog
Index of all articlesRational Recursive (-Iterative) Forms
Some pictures (the beauty of lapse):


Recursive Forms? (I did not find examples on the internet, so this name came up to me. My way to numbers is by computer experiments and pictures, so other attributes might heve been ‘generative functions’, ‘recursive functions’ aso.) The Ideas behind this stuff are so simple, that I’m quite sure, that someone else might have come up with. So for example the Tribonacci sequence (and some n-bonacci sequences) are part of The On-Line Encyclopedia of Integer Sequences On the other side there are exploding many recursive forms and the only referenz I found was Wolfram’s ‘New Kind of Science’ (the NKS pictures that stayed in my mind are syntactic recursive forms) where was stated, that there is a lack of systematical investigation of this stuff.
Caution: This text is not mathematically strict. This is just part of my daily disport and belongs to the publications of the ANM (academy of naive mathematics).
I think this forms must be investigated systematically. They are beautifull, surprising and may have many connections to so many things… (Mistakes, Growth, Precission, Quantumtheorie?, Philosophy)
What catched me!
While thinking about the Fibonacci sequence and its general form Lucas sequences, I came up with the idea to check complexer additive forms.
So if the fibonacci sequence and some lucas sequences (not all, but I don’t want to complicate things now) could be represented by [f=[a,b]; append f[-2] + f[-1] for ever] or an other way to write [[a,b]; a + b], which results in
- (1)a
- (1)b
- (1)a+(1)b
- a+2b
- 2a+3b
- 3a+5b
- 5a+8b
- etc. with the factors of a and b giving 2 times the fibonacci sequence [1,1,2,3,5,8,13,...] and the sums at each line with [a,b]=[1,1] give also the same sequence.
This sequences grow quite fast and were studied by real mathematicans in deep. If you change the starting values of a and b you will get other sequences (lucas, but not all I think), but the structure stays somehow the same (fibbonacci is always there, so may be we can call these: representations of simple growth processes)
My next step was, to extend the starting values to something like [a,b,c,...] and to add subtraction. So we get for example forms like:
- [[a,b,c]; ( + / – )f[-3] ( + / – )f[-2] ( + / – )f[-1]]
There are many sequences of this form. For example [[a,b,c]; a + b + c] or [[a,b,c]; – a + b – c] and so on. There is a simple way to generate al this forms up to n varaibles. Simply count in ternary system starting with 1 and say 1:= + 1, 2:= – 1 and 0:=0:
So there are 2 forms with one variable:
- 1 = a
- 2 = -a
there are 6 forms with 2 variables [starting array has 2 values]:
- 3 (10) = +b ;(0a)
- 4 (11) = +b +a
- 5 (12) = +b -a
- 6 (20) = -b
- 7 (21) = -b +a
- 8 (22) = -b -a
there are 3n – 3(n-1) forms of n varables, so it goes on with:
- 9 (100) = +c
- ...
- 13 (111) = +c +b +a
- 14 (112) = +c +b -a
- and so on.
Next step I did: I wrote a program that systematically built sequences based on these recusion formulars with the starting array [1,1,1,...] and I got some nice sequences but in most cases they are growing (+ or – or both infinities), so I did the genaral case and wrote a program that started with [a,b,c,...] and built the symbolic sequences, which again gave nice results with fast growing factors of a,b,c and so on.
There are many nice resultes, so here one example [[a,b,c,d];a+b-c+d]:
- a
- b
- c
- d
- a+b-c+d
- a+2b
- b+2c
- c+2d
- 2a+2b-2c+3d
- 3a+5b-c+d
- a+4b+4c
- b+4c+4d
- 4a+4b-3c+8d
- 8a+12b-4c+5d
- and so on
which gives 1,1,1,1,2,3,3,3,5,8,9,9,13,21,26,27,...
In my programm I represented these sequences without those [a,b,c,...] so that they could be given as follows.
Fibonacci:- Sum [as,bs]
- 1 [1,0]
- 1 [0,1]
- 2 [1, 1]
- 3 [1, 2]
- 5 [2, 3]
- 8 [3, 5]
- 13 [5, 8]
- 21 [8, 13]
- 34 [13, 21]
- 55 [21, 34]
- 89 [34, 55]
- 144 [55, 89]
But really interessting are those:
5 Parameters which factors grow but sum is allways 1:
- 1 [1, 0, 0, 0, 0]
- 1 [0, 1, 0, 0, 0]
- 1 [0, 0, 1, 0, 0]
- 1 [0, 0, 0, 1, 0]
- 1 [0, 0, 0, 0, 1]
- 1 [0, 1, -1, 1, -1]
- 1 [-1, 0, 2, -2, 2]
- 1 [2, 1, -2, 4, -4]
- 1 [-4, -2, 5, -6, 8]
- 1 [8, 4, -10, 13, -14]
- 1 [-14, -6, 18, -24, 27]
- 1 [27, 13, -33, 45, -51]
- 1 [-51, -24, 64, -84, 96]
- 1 [96, 45, -120, 160, -180]
- 1 [-180, -84, 225, -300, 340]
- 1 [340, 160, -424, 565, -640]
- 1 [-640, -300, 800, -1064, 1205]
- 1 [1205, 565, -1505, 2005, -2269]
- 1 [-2269, -1064, 2834, -3774, 4274]
or:
- 1 [1, 0, 0, 0, 0]
- 1 [0, 1, 0, 0, 0]
- 1 [0, 0, 1, 0, 0]
- 1 [0, 0, 0, 1, 0]
- 1 [0, 0, 0, 0, 1]
- 1 [1, 1, -1, -1, 1]
- 1 [1, 2, 0, -2, 0]
- 1 [0, 1, 2, 0, -2]
- 1 [-2, -2, 3, 4, -2]
- 1 [-2, -4, 0, 5, 2]
- 1 [2, 0, -6, -2, 7]
- 1 [7, 9, -7, -13, 5]
- 1 [5, 12, 4, -12, -8]
- 1 [-8, -3, 20, 12, -20]
- 1 [-20, -28, 17, 40, -8]
- 1 [-8, -28, -20, 25, 32]
- 1 [32, 24, -60, -52, 57]
- 1 [57, 89, -33, -117, 5]
- 1 [5, 62, 84, -38, -112]
- 1 [-112, -107, 174, 196, -150]
- 1 [-150, -262, 43, 324, 46]
- 1 [46, -104, -308, -3, 370]
So this is iteressting and I think group theorie would be a nice framework to investigate this stuff, but the next idea came over me.
Combinig the forms to rational forms, we are entering Q
I allways thought, that Q (Rational numbers) is a good trick to see something that Z (N) hides. Q is like Z but maped to our perspective. Ok with a little bit lost, but … So the Idea was to combine the additive forms to rational forms. What happens if the reursion rule divides the additive forms?
This means
- [[a,b,c,...]; X / Y]
where X,Y are any additive formes over [a,b,c,...]. So I wrote a programm that does this for some forms and checked them. Ok, the results were lists of rational numbers, but the trick is to visualize them. This was done with gnuplot and here is the point where the real story begins. I played around with the starting values and got this beautifull pictures, that I animated:
This is [[a,b,c]];a + b / c] for [a,b,c] = [[2,1.01,2],[2,1.02,2]...[2,2, 2]... [2,5.01,2]] and [[200,0.01,200],[200,0.02,200] ...[200,1.01,200]] and this is wrong!. But on the beauty of lapse later more. (I’m using Ruby and Python and did my first experiments with real rational numbers that are included in this languages, tried out floating points and got the same reaults, but my fault was, that I did only 10 iterations, so my first pictures are based on floating point arithmetric, and this is dangerous)
So let’s do more forms
Next I wrote a program that systematically generates all rational forms from 2 up to 5 variables. Now combinatorical explosion comes in. I got – after removing equvalent forms – 22 2-forms, 310 3-forms, 4132 4-forms and 29116 5-forms of the form X/Y where X,Y are simple additive forms up to 5 varables. So here some examples:
2-1 a/(a+b) f[-2]/(f[-2]+f[-1]) 2-2 a/(-a+b) f[-2]/(-f[-2]+f[-1]) 2-3 a/(a-b) f[-2]/(f[-2]-f[-1]) 2-4 a/(-a-b) f[-2]/(-f[-2]-f[-1]) 2-5 b/(a+b) f[-1]/(f[-2]+f[-1]) 2-6 b/(-a+b) f[-1]/(-f[-2]+f[-1]) 2-7 b/(a-b) f[-1]/(f[-2]-f[-1]) 2-8 b/(-a-b) f[-1]/(-f[-2]-f[-1]) 2-9 (a+b)/a (f[-2]+f[-1])/f[-2] 2-10 (a+b)/-a (f[-2]+f[-1])/-f[-2] 2-11 (a+b)/b (f[-2]+f[-1])/f[-1] 2-12 (a+b)/(-a+b) (f[-2]+f[-1])/(-f[-2]+f[-1]) 2-13 (a+b)/-b (f[-2]+f[-1])/-f[-1] 2-14 (a+b)/(a-b) (f[-2]+f[-1])/(f[-2]-f[-1]) 2-15 (a+b)/(-a-b) (f[-2]+f[-1])/(-f[-2]-f[-1]) *is this -1?* 2-16 (-a+b)/a (-f[-2]+f[-1])/f[-2] 2-17 (-a+b)/-a (-f[-2]+f[-1])/-f[-2] 2-18 (-a+b)/b (-f[-2]+f[-1])/f[-1] 2-19 (-a+b)/(a+b) (-f[-2]+f[-1])/(f[-2]+f[-1]) 2-20 (-a+b)/-b (-f[-2]+f[-1])/-f[-1] 2-21 (-a+b)/(a-b) (-f[-2]+f[-1])/(f[-2]-f[-1]) *is this 1?* 2-22 (-a+b)/(-a-b) (-f[-2]+f[-1])/(-f[-2]-f[-1]) 3-1 a/(a+b) f[-3]/(f[-3]+f[-2]) 3-2 a/(-a+b) f[-3]/(-f[-3]+f[-2]) ... 3-309 (-a-b+c)/(a-b-c) (-f[-3]-f[-2]+f[-1])/(f[-3]-f[-2]-f[-1]) 3-310 (-a-b+c)/(-a-b-c) (-f[-3]-f[-2]+f[-1])/(-f[-3]-f[-2]-f[-1]) 4-1 a/(a+b) f[-4]/(f[-4]+f[-3]) 4-2 a/(-a+b) f[-4]/(-f[-4]+f[-3]) 4-3 a/(a-b) f[-4]/(f[-4]-f[-3]) ... 4-3132 (-a-b-c+d)/(-a-b-c-d) (-f[-4]-f[-3]-f[-2]+f[-1])/(-f[-4]-f[-3]-f[-2]-f[-1]) 5-1 a/(a+b) f[-5]/(f[-5]+f[-4]) 5-2 a/(-a+b) f[-5]/(-f[-5]+f[-4]) ... 5-29116 (-a-b-c-d+e)/(-a-b-c-d-e) (-f[-5]-f[-4]-f[-3]-f[-2]+f[-1])/(-f[-5]-f[-4]-f[-3]-f[-2]-f[-1])
2-15 and 2-21 is this + / – 1?: Here some mathematical advise would be fine, because I see that this forms reduce to a constant function, but if you use them recursivly, -1 becomes constant but +1 becomes to 0/0 which is not defined. One way would be to exclude starting values where a-b or -a+b = 0. (but this is marginal and my programs simply stop calculating, when a division by zero exception occures.)
Next I wrote a program that genarates an example picture of each form. And when I started this program, I had very exciting 3 hours:
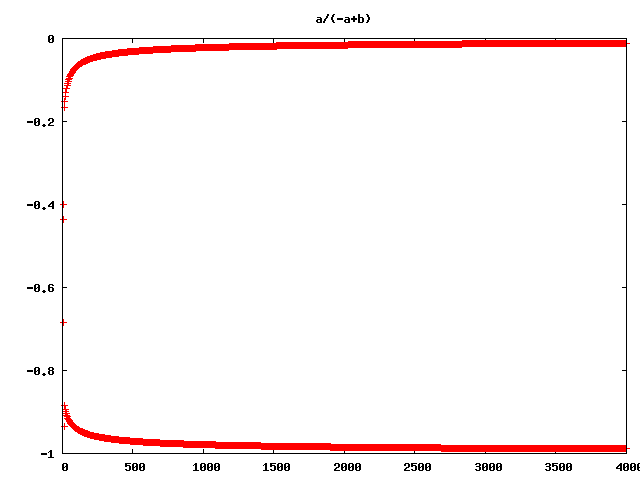
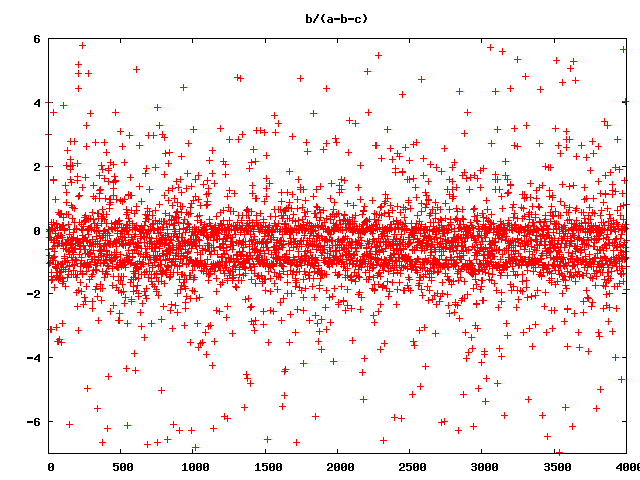
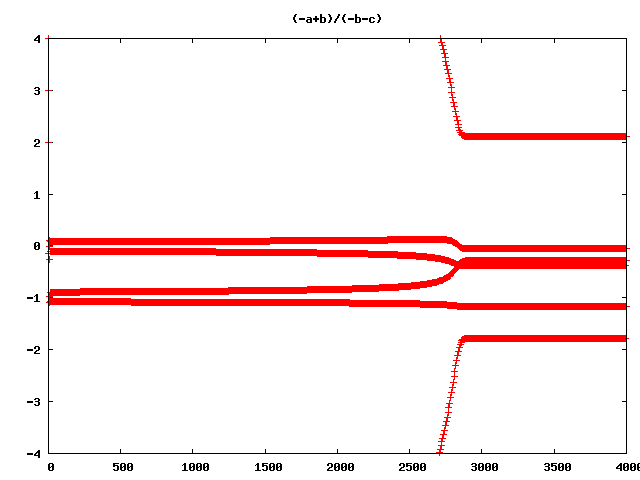
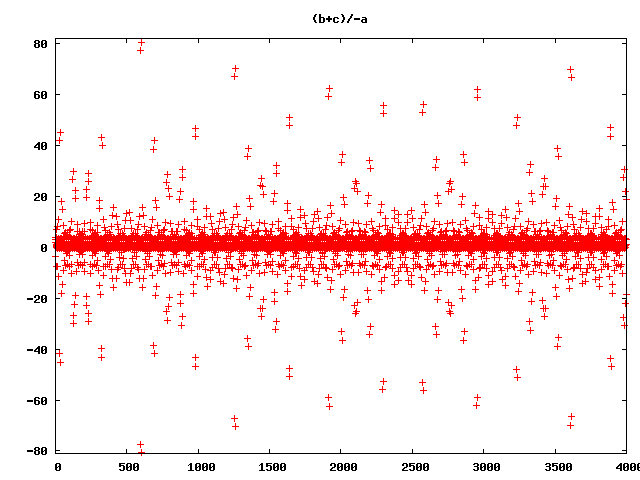
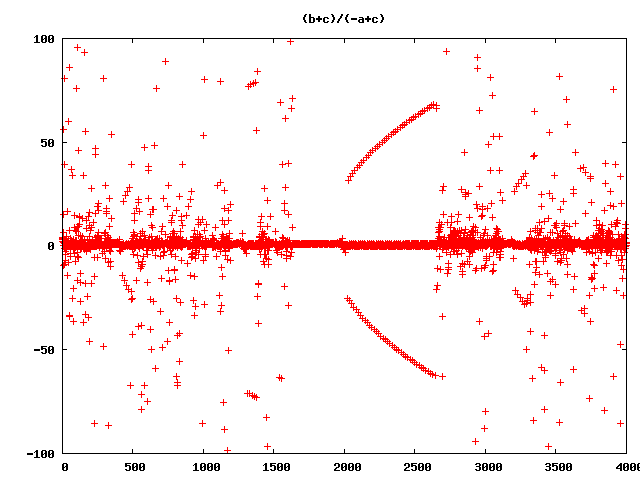
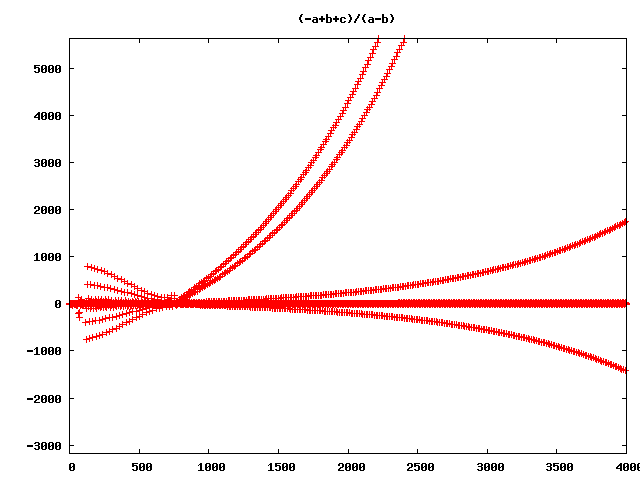
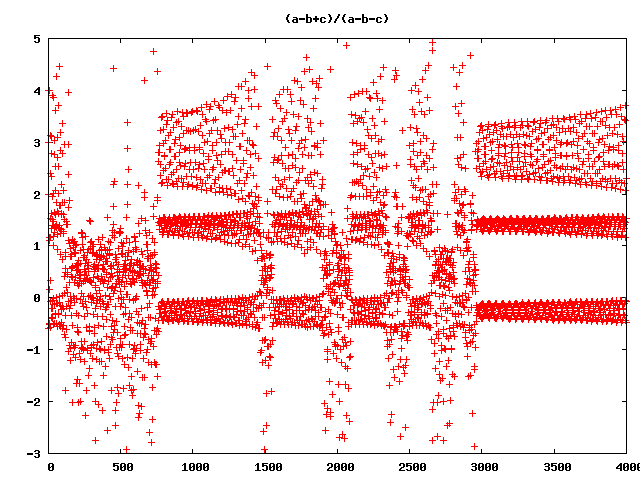
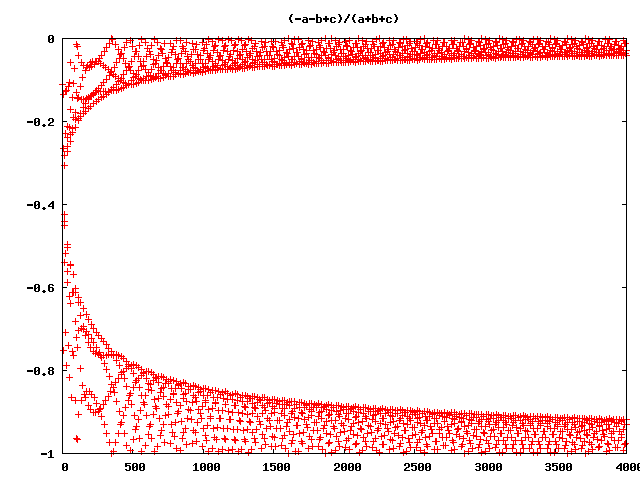
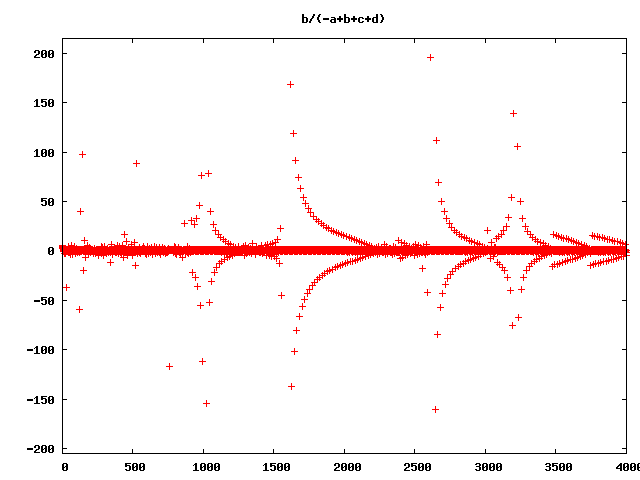
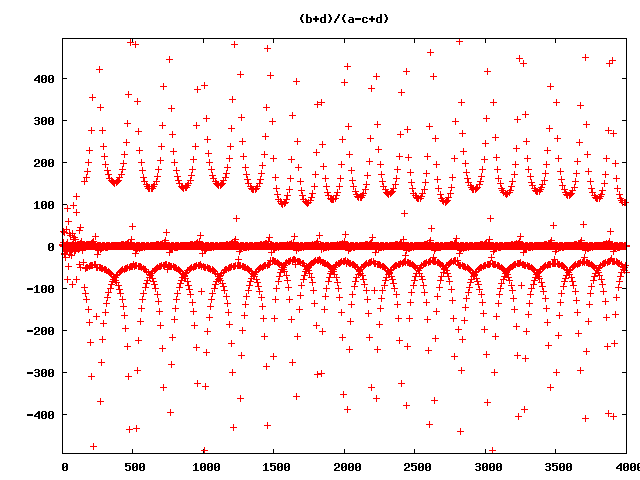
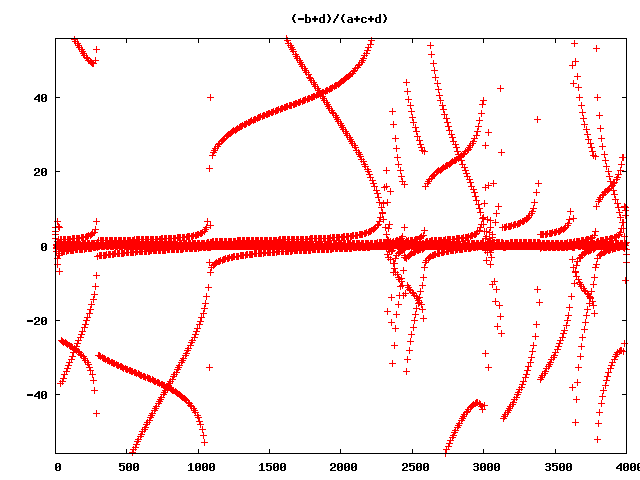
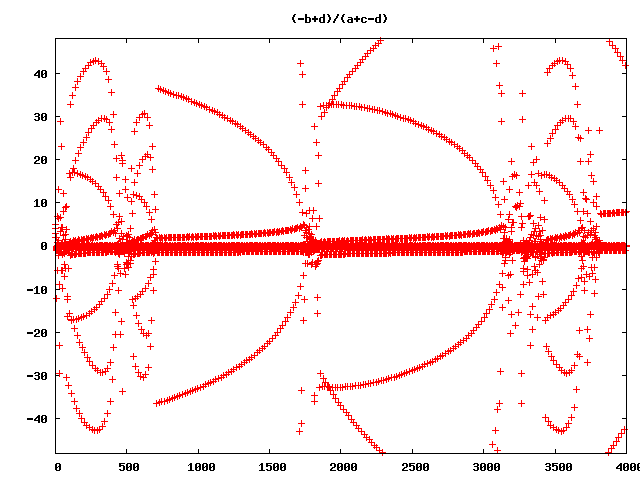
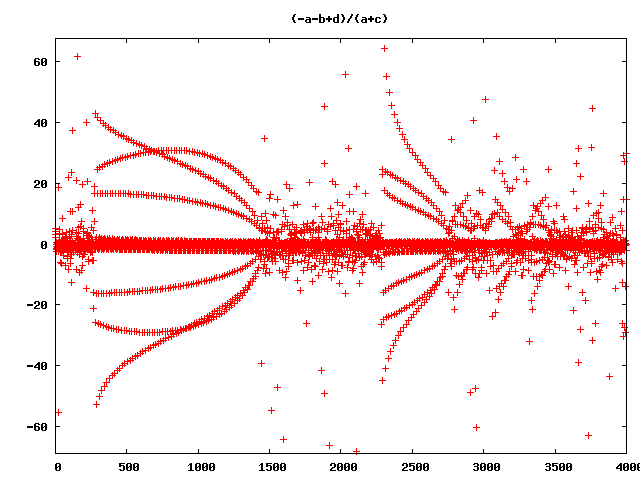
and so on and so on … (Wow!)
But still wrong ;-)
So what’s wrong with all this pictures?
They are not the right visualisations of the rucursive forms! Ok, I allways had in mind, that floating point arithmetric is full of pit falls. So I decided to do some checks, with much higher precission. First, I tried real rational numbers. No chance! The numerators and denominators grow extremly fast and after 50 Iterations the program slows down extremley and my pics are based on 4000 iterations. But in many cases with the rational recursive forms the ranges of numerator and denominator are near together, so there is a chance, that the errors are not so big, that the pictures will be absolute senseless. So I tried out another datatype. Python and Ruby have a Deicimal Type with arbitrarry precision, that can be limited to a certain precision. I wrote a program that iterated over precision, to see what happens if we go from 28 to 3000 significant numbers. It came out, that in most cases 300 significant numbers may be enough. Although I am not sure, if there are more hidden lapses, here is an animation of the precision iteration:
So in this case after precision is 80 the form stays stable. I hope that this is right now, but I’m still evaluating an testing.
To find out interssing forms, as a first shoot floating points are quite well and the wrong pics are beautyfull too!
here some examples of higher dimension
will be continued …
- dimensions to walk through: starting values (a,b,c,...), focus (y axe), iterations (x axe), precision
- just started to investigate more generally the builing blocks: [[a,b,...]; p(n)f[-n] + ... + p(1)f(1) + p(0)].
 muzuu.org ist im Besitz von Kizuu, welche ein Produkt von Zuufuzu ist. Kontakt:
muzuu.org ist im Besitz von Kizuu, welche ein Produkt von Zuufuzu ist. Kontakt: